Science Talk: Towards a New Paradigm

Part II – The Subtle Planes of Matter

As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality.

Albert Einstein

This essay is to notify interested readers that there is a mathematical model which currently exists within electromagnetic theory which provides an explanation of certain subtle energy phenomena and fits within the current science framework. However before we discuss theories that are being worked on at present, I want to examine the scientific view of energy in general and offer some basic definitions.

Central to the issue of vibrational medecine and complementary practices is the recognition of the role of energy. Knowing this however does not necessarily enlighten us because as yet there is no consensus agreement as to the nature of energy itself. Ask any physicist the question "What is energy?" and they will probably start out talking about how it is involved in physical processes such as the falling of objects, chemical reactions, radioactive decay and so on. At this point they should have paused in realisation that this is not what energy actual is but ways in which it manifests. The late Richard Fenyman, the much respected physicist, was keenly aware of this deficit and purposefully wrote that: "Scientists fail to admit that they do not have the slightest idea what energy is." If the modern consensus does not agree on this matter then where can we look for understanding on this matter? The Greeks seemed to have enjoyed better insight into the nature of energy by virtue of the very root from which the word energy derives, 'en ergos' meaning in motion. From this awareness of energy as somehow linked to motion and change, we might form a more useful definition of energy as that which induces a change of state. This covers its function in all domains of reality, from the physical interactions that science is so familiar with to changes in mental and emotional states and deeper levels of consciousness. Energy then is the process of change itself, masquerading under various forms that relate one state of a structure to another. Now we can talk about healing and spiritual energy without being accused of dealing in abstractions and the indefinable. If a change of state has occurred, at any level of being or reality, then energy must have been involved in the process.

Skip Science Definitions

Science Definitions

REFERENCE POINT: Reference Point is defined as being one of two or more predetermined and specific points between which, measurements are to be made.

MOTION: Motion is defined as a continuing change in the relative position of a given object or reference point, with respect to the observer, or to some other object or reference point. Everyone has a tendency to think of motion as being something absolute. Either a body moves, or it does not move. Yet, if we look about us at the universe, we find that every body of matter in the universe is in motion. They are all in motion with respect to us, and each of them is in motion with respect to every other body. Where can we find a reference point from which to determine absolute motion? It must be understood that when we speak of motion, we are using as a purely relative term. When we say that an object is in motion, we mean only that its present position is changing with respect to us, or to some other specified object, or point of reference.

VELOCITY: Velocity is defined as the rate of motion. It is measured by the amount of change in position which occurs in a given unit of time. Velocity is usually measured in miles per hour. or centimeters per second. Whatever the unit used for its measurement, however, we must always remember that if it is to have any significance, the measurement must be made from a specified point of reference or observation. For example, we can easily see that a man seated in his easy chair at home, has zero velocity with respect to the earth, but considerable angular velocity with respect to the moon, a much higher velocity with respect to the sun, and a different and still higher velocity with respect to each of the countless stars in the known universe.

ACCELERATION: Acceleration is defined as a change in the existing state of motion. It can be either positive or negative. That is: if the observed velocity is increasing, the acceleration is said to be positive. If the velocity is decreasing, the acceleration is said to be negative. (The word deceleration is sometimes used to indicate a decreasing velocity, but the term negative acceleration is generally considered to be more proper.) Example: If a certain automobile were to >speed up=, from ten miles per hour to sixty miles per hour in a period of ten seconds, we would say that its velocity had increased at a rate of five miles per hour during each second of acceleration. We would indicate this by saying that its acceleration was equal to five miles per hour, per second. In physics, acceleration is usually measured in meters or centimeters per second, per second. In mathematics this is usually written - Cm/S/S, or Cm/S2.

ENERGY: We will define energy as the ability to create changes in the position or condition of objects or points of reference. However, energy can create change, only when there exists a differential in the two points between which the change becomes manifest, or when the unit of energy has become divided into its two component parts called poles, or charges. One positive and one negative pole or charge, when united, constitute one photon or quantum of energy.

FIELD: A field is an area of influence which surrounds the poles of energy when they are separated. The field manifests itself as a force which tends to increase the distance between like poles or charges, and to decrease the distance between unlike, or pairs, of poles or charges. The field is usually divided into three general types, the Electric Field, the Magnetic Field, and the Gravitational Field. The three types, however, are simply special case manifestations of the field principle, and all three result from the division of energy into its two component parts.

MASS: Mass is a property which is usually associated with matter, but which is also found to be associated with energy. It is defined as the property of resistance to acceleration, and is measured by the amount of force required to produce a given rate of acceleration. All matter has the property of mass, but not all mass has the property of matter. We must distinguish carefully between matter and mass. Further clarification will be given later in the text.

SPACE: Space is defined as that which separates bodies of matter. Space has no objective reality except as an order or arrangement of the objects we perceive in it.

TIME: Time is defined as that which separates events. It is the one dimension in which all motion must take place. Note that this definition will not preclude the quantum fact of non-locality or action at a distance.

The series of mathematical formula which Albert Einstein gave to the world in 1905, he called "A Theory of Special Relativity". Einstein brought to our attention that the factors of Gravity, Space, Time and Energy were not absolute and independent entities, but that they were variable factors, each having a value which depended upon the value of others.

In almost every text book on physics in the world today the statement is made that the quantity C represents the velocity of light (in centimeters per second), yet every student in the world who has studied the subject, knows that the velocity of light is not a constant. That its velocity, in fact, varies slightly with each different medium through which it is propagated. Any student who has ever passed a beam of sunlight through a prism to produce a spectrum of color, has demonstrated that not only does the velocity of light vary in different media, but that the change in velocity varies somewhat with the frequency of the light when propagated in material media. This of course is the principal upon which all of our spectroscopes are designed, although most textbooks state merely that the light is refracted or `bent' in passing from one medium to another. There are many who will dispute the statement that the change in velocity varies with the frequency, but when sufficiently precise tests are made entirely within a single medium, the results indicate convincingly that this is true.

Spectrum made visible by Dispersion with a Prism

At this point most students will remark that the quantity C refers to the velocity of light in a perfect vacuum, but where in the universe can we find a perfect vacuum in which to test this assertion? Astronomers and physicists have estimated that even in the remotest depths of intergalactic space there will probably be found, from three to seven nuclear or atomic particles per cubic centimeter. A beam of light traveling at approximately 3x10¹⁰ centimeters per second would still encounter a rather large number of such particles during each second of its journey. While it is true that the proportionate decrease in velocity which would be produced by this minute concentration of matter is so small that it might be negligible for all practical purposes of measurement, nevertheless it demonstrates the fact that we have chosen as our sole remaining constant, a quantity which actually can never be a perfect constant anywhere in the know universe.

Fortunately there is a value to which the quantity C can be assigned which is a constant. Moreover the assignment of the quantity C to this factor makes possible a much better understanding of the natural laws involved in the propagation of energy. The quantity C is actually the kinetic energy equivalent of the mass energy of matter. In other words, if we take a gram (or any other quantity of matter: Newtonian mass) and convert that matter gradually into energy according to the formula E=mc², and the resultant energy, as it appeared, were constantly applied to the remaining matter in such a way as to accelerate it uniformly in a given direction, when all the matter had been so converted we would find that we had zero Newtonian mass, infinite inertial mass and a resultant velocity equal to the quantity C, or approximately 3x10¹⁰ centimeters per second (with respect to the given reference or starting point). The maximum velocity attained would always be the same regardless of the quantity of matter with which we started. This is a fact which can easily be verified by anyone who is mathematically inclined, and who is familiar with the laws of acceleration. The energy required to accelerate each gram of mass to the velocity C through energy conversion is exactly equal to total energy inherent in any matter having that mass.

This fact forms the true basis of the statement in our present day physics that the velocity C is a maximum or limiting velocity, since it represents the greatest kinetic energy differential which can exist between two given reference points. Another assumption in the theories of relativity given to the world by Dr. Einstein, the natural laws, in general, are assumed to be linear, but the space in which they operate is considered to be "curved". This concept offers the simplest mathematical presentation, since all of the deviations from linearity can thus be explained by a single postulate. Unfortunately, like most of our mathematical presentations, the concept offers but little for the mind to grasp. A curved space cannot be pictured mentally, nor can it be drawn upon paper. The question always arises, if space is inside the curve, what is outside?

We have discovered that the linear mathematics which we commonly apply to the rules of nature, do not hold true when carried to an extent which permits the error to be measured, because they do not follow a straight line reaching to infinity, but a curve of finite radii. In a timeless universe, this curve, in any given plane, would be represented by a circle, but since the laws operate through time as well as space, the curve may be more readily understood if depicted as a "sine curve" or "wave". The "base" line of the wave (which is the center line of the curve) represents zero, and the portions above and below the line represent the positive and negative aspects of the law. Thus we see that there are points and conditions in which the natural laws reach zero value with respect to a given reference point, and that beyond these points the laws become negative, reversing their effect with respect to the observer.

The constant repetition of the term "reference point" or "observer" is necessary to emphasize the frequently unrecognized fact that none of the basic factors of nature have any reality or significance except when considered from a specified position or condition. If, therefore, we exchange the existing mathematical postulate of linear laws operating in a curved space, for a concept based upon the curvature of natural law, we will find that we have not invalidated or changed any of the presently accepted mathematics which we apply to these concepts. They can still be applied in the same way, and will give the same results.

By the exchange, however, we will have achieved a position from which the operation of the natural laws can be pictured by the mind, and can be charted upon paper. It will be helpful for the reader to examine at this time, a more advanced, yet contemporary model in the existing framework of science, for comparison purposes. The easiest way to the unknown is through the known.

Although most contemporary scientists would offer the assumption that no mathematical models currently exist within electromagnetic theory to explain the existence of scalar vectors as a fundamental originating force in vacuum (or ether), there are an increasing number of prominent researchers revisiting this area. Those In the forefront, notably, Thomas Bearden, Moray King, Henry Monteith, Paul LaViolette and Shinichi Seike, are taking a closer scrutiny of the pioneering work of E.T. Whittaker, Nikola Tesla, T.T. Brown and Burkhard Heim. The list certainly is not exhaustive. One such researcher is Dr. William Tiller, a professor at Stanford University and former chairman of the department of Materials Science. It is his model we are looking at.

Dr William Tiller has spent over a decade on a theory that others are now calling the Tiller-Einstein Model of Positive - Negative Space/time. Richard Gerber calls it the Tiller-Einstein Model because it's insights are basic to the Einsteinian equation relating energy to matter from which it is derived. The most familiar form of this equation is as follows: E=mc², however this is not the entire expression. The shorter equation is modified by a proportionality constant known as the Einstein-Lorentz Transformation. This transformational constant is the relativistic factor that describes how different parameters of measurement from time distortion to alteration of length, width,and mass will vary according to the velocity of the systems being described the true Einsteinian equation is as below:

Diagram 1
Einstein-Lorentz Transformation

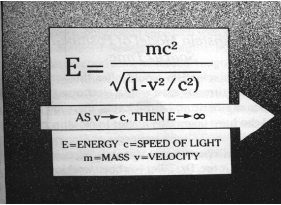
The classical interpretation of Einstein's famous equation is that the energy contained within a particle is equivalent to the product of its mass multiplied by the speed of light squared. This means there is an incredible amount of potential energy stored within a tiny particle of matter. A more complete understanding of Einstein's equation has evolved over time which may begin to help scientists comprehend the multi-dimensional nature of the universe. Einstein's equation suggests that matter and energy are interconvertable and interconnected. Subatomic matter is actually a form of condensed particularized energy i.e. a frozen mini-energy field. The atomic bomb is one example how matter can be converted into energy. When one examines the extended equation above in which E=mc² is modified by the Einstein-Lorentz Transformation new insights into the dimensional aspects of matter both gross and subtle matter can be appreciated. If one accelerates a particle faster and faster until it approaches the speed of light its kinetic energy increases exponentially as described by the equation K.E.=½mv², where v is velocity. see diagram below.

Diagram 2
Relationship of Energy to Velocity

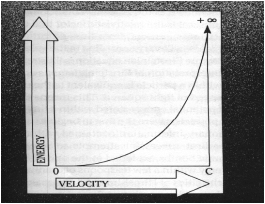
An interpretation of this relationship could make it seem that it is physically impossible to accelerate particles beyond the speed of light. The ascending curve approaches the speed of light (c) but never intersects with it and continues off into infinity. High energy physicists are aware that as one tries to accelerate a subatomic particle faster and faster close to the speed of light, extremely large amounts of energy are needed. The reason is because the relativistic mass of a particle increases exponentially at speeds approaching light velocity, until the energy needed for further acceleration to 'c' becomes tremendous. This tremendous energy is what is necessary to accelerate a physical particle of matter. Physicists have accepted the seeming limitation that one cannot accelerate matter beyond the speed of light. This assumption is partly related to the fact that when one inserts numbers greater than the speed of light into the Einstein-Lorentz Transformation one arrives at the solutions containing the square root of -1, which is considered an imaginary number. Here we face a wall of unbelief by physicists who do not believe in imaginary numbers, they assume that the speed of light is the maximum velocity at which matter can travel. However there are a few renegades who believe differently.

Pioneering mathematician Charles Muse¹ considers the square root of -1 to be a category of numbers referred to as "hypernumbers." These hypernumbers are necessary to the development of equations which described the behaviour of higher dimensional phenomena (such as the subtle energy interactions of living systems). Muse points out that even though imaginary numbers like the square root of -1 may seem impossible to fathom, they are necessary to find solutions in the equations of electromagnetic and quantum theory.

We make the assumption that solutions containing the square root of -1 may be valid in describing higher dimensional phenomena. This allows us to begin to understand the full predictive power inherent in the transformed Einsteinian equation. The diagram below is a plot of the energy of a paricle relative to it's velocity from a particle relative to its velocity from a theretical state of rest all the way to beyond the speed of light (c).

Diagram 3
Positive-Negative space/Time Model

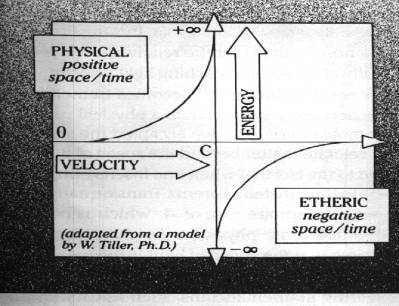
The Mathematical derivation is described as follows:

Skip Mathematical derivation

The Tiller-Einstein Model of Positive-Negative Space/Time

In the above equation Einstein-Lorentz Transformation we see that energy is related to matter according to the proprtionality constant containing the ratio . As velocity (v) of a particle approaches the speed of light (c) then this ration approaches 1. If one substitutes into (v) a velocity equalling 99.995 percent of the speed of light, then the ratio v²/c² is close to 1 (actually 0.9999). The figure within the square root sign shows that we must subtract our previous solution from 1 : 1-0.9999=0.0001. The square root of 0.0001 is equal to 0.01. This solution must now be inverted because it exists in the equation as the denominator of the fractional expression, therefore 1/0.1=100. This means that at a velocity of 99.995 percent of the speed of light, the associated energy calculated from the expression mc² must be multiplied by 100. As velocity goes even higher, and even closer to light velocity, the amplification factor becomes exponentially great. The visual expression of this relationship is displayed in Diagram 1.

Remember we are discussing the energy required to accelerate a "physical" particle. If we examine the equation again but this time substitute a velocity greater than light, where v is greater than c. Because the ratio v²/c² is now greater than 1, 1 minus a number greater than 1 is equal to a negative number. One ends up with an equation that has a denominator containing the square root of a negative number. This may be factored out to be apositive number times the square root of -1. This number has been called "i" by mathematicians. It is a factor which can be substituted for the square root of -1 (for ease in dealing with difficult equations). The square root of -1 is considered an imaginary number by most individuals dealing with numbers. As stated already, Muse points out that even though imaginary numbers like the square root of -1 may seem impossible to fathom, they are necessary to find solutions in the equations of electromagnetic and quantum theory.

We are interested in the behaviour of matter and energy as described by the Einstein-Lorentz Transformation. When we are dealing with systems whose veolcity exceed the speed of light. When we substitute veolocities greater than light in the equation a second inverted curve appears with a mirror-like symmetry to the first. Whereas the first curve begins at the zero axis and climbs toward positive infinity (+ infinity), the second curve begins at the negativity (- infinity) and returns back to the zero axis. Tiller refers to matter described by the curve to the left of c, (at velocities less than the speed of light) as the world of Positive Space/Time (+S/T) and the world of Negative Space/Time (-S/T) where energy is magnetoelectric and negativity entropic, and substance is of a subtle magnetic character. Negative is the dimension of the etheric world of energies which includes the human etheric body. The substance which makes up our etheric bodies vibrates at speeds faster than light making it difficult to directly measure with convention electromagnetic sensing equipment. It is theorized that the astral world also exists within the negative space/time dimension at vibratory speeds exceeding those of the etheric. The developed clairvoyant is able to perceive these subtle energies because he or she is able to able to take in energy via the etheric and astral chakras, which act as organs of perception on the appropriate levels of reality.

A number of physicists have proposed the existence of a particle known as a "tachyon", which would theoretically exist only at speeds exceeding that of light velocity². The properties of such unusal particles at faster than light velocity are quite interesting. Unlike Positive Space/Time matter which is associated with forces of electricity and electromagnetic (EM) radiation. -ve Negative Space/Time is associated primarily with magnetism and a force which Tiller describes as magnetoelectric (ME) radiation. Electromagnetic theory predicts that magnetic monopoles- particles magnetically charged either North or South should exist in nature. No one has yet successfully captured or repeatedly detected magnetic monopoles. It is possible that if a domain of this particle is in tachyonic realms like those in Tiller's negative space/time model, then our present measuring equipment may be inadequate(or insensitive) for the task. As all solutions to the Einstein-Lorentz Transformation at supraluminal (faster-than light) velocities are negative in character, then negative space/time matter would have negative mass and demonstrate the property of negative entropy. Entropy is a term which describes the tendency toward disorder. In general, most systems within the physical universe tend toward increasing positive entropy and more disorder over time. However the most notable exception to this rule is living systems. Biological systems take in raw material (food) and organize these simple components into complex macromolecular structures (such as protein, DNA, collagen etc.). Living systems display the property of negative entropy, or a tendency toward decreasing disorder of the system. One may say the life-force seems to be associated with negative entropic characteristics. (When a body dies and the life force vacates the physical form, the remaining unoccupied shell returns, via earthly microorganisms to its raw constitutents, in characteristic positive entropic style.)

Is life, then, particularly developing life, somehow connected to the universe of negative space/time and the energies that may be found there? Kirlian photography is a good tool to further look into this possibility.

To produce a Kirlian photograph (also known as an electrograph), a high-frequency power source is connected to an electrode beneath a sheet of film, creating an electrical field of high potential that bathes the film. When a grounded object is placed on the film in complete darkness, the electron trails created by electrons flowing from the charged plate to the grounded object create an image. Just as an MRI produces diagnostically valuable results only when the frequency of the apparatus is set to resonate with hydrogen, the discharge corona produced by a Kirlian photograph is significant only when the frequencies of the power source resonate with the negative space/time frequencies involved in biological system.

Understanding this seems to be the key in replicability of Kirlian photograph experiments, such as the "phantom leaf." If a piece of a leaf is removed and the remaining leaf is grounded and placed on a Kirlian plate, the resulting image is still that of the entire leaf. What is more, if the vein side of the leaf is placed against the plate, the image of the missing portion is of the veined side of the leaf. If the pore side is photographed, it is the pore side of the missing portion that produces an image. This would be equivalent to slicing off the upper fingers of a hand and taking electrographs of the front and back of the hand. One electrograph would show phantom fingerprints, and the other would show phantom fingernails. The spatial and organizational properties of such a biological energy field would seem to be holographic in nature (2). This supposition is further evidenced if the missing piece of the leaf is a circle removed from the center. The resulting electrograph reveals a leaf with the circle, which contains an image of the entire leaf with a circular hole in the center containing a tinier leaf.

Dr. Harold Burr discovered that, in plant seedlings, the contour of the electrical field surrounding the new sprouts followed the shape of the adult plant. Taken together with the results from Kirlian photography experiments, we might now surmise that there is indeed some sort of holographic energy field that provides guidance and spatial orientation to the rapidly developing tissues and organs of an embryo - an energy field template(3). This energy field is often referred to in vibrational healing as the "etheric body."

The etheric body a self-organising holographic energy template, would also seem to demonstrate negative entropic properties. The etheric body supplies the spatial ordering properties to the cellular systems of the physical body. This negatively entropic characteristic of the subtle life-energies and the etheric template would appear to satisfy at least one requirement of Tiller's negative space/time matter.

In addition negative space/time is primarily magnetic in nature. In Bernard Grad's experiments on the effects of laying on of hands healing on living systems, it was discovered that the growth rate of plants could be accelerated by magnet-treated water as well as healer treated water. A number of other similarities between magnet- and healer-treated water have also been found. Research chemist Robert Miller found that copper sulfate dissolved in regular distilled water forms jade-green monoclinic crystals when it precipitates out of solution. If the copper sulfate solution is exposed to the energies of a healer's hands or a strong magnetic field it always forms coarser grained turquoise-blue crystals, instead of the characteristic jade-green crystals.³

Kirlian Aura Images of Two Drops of Water

One of the most fascinating research directions on Earth at present is the study of the Aura and bio-energetic structure of water. This research is conducted in Russia by Prof. K.Korotkov.

Two Kirlian Aura images of seemingly identical drops of water, kindly provided by Prof Korotkov, are shown. The left image depicts Aura vibration around a drop of normal water and the right image shows the Aura around a drop charged by the famous Russian healer Allan Chumak during ten minutes of conscious concentration. The difference in the bio-energy glow is dramatic: the bio-charged water has more than 30 times stronger Aura vibration and significantly altered physical and biological properties.

Contemporary physics cannot explain the above change in water glow which, technically speaking, is a purely physical process involving an electrical discharge in air around the drop. The main reason for this is that a great majority of “scientists” on Earth completely ignore our consciousness in their perception of Reality. Prof. K.Korotkov says that the increase in the Aura around a drop of water cannot be explained without considering the energy and vibration of our consciousness. Water Aura experiments are indisputable evidence that our mind, when properly trained, can dramatically change the qualities of matter.

Studies by Dr. Justa Smith⁴a nun and biochemist working at the Human Dimensions Institute at Rosary Hill College in New York, found that the healer was able to increase the enzyme reaction rate over time, and that the longer the healer held the test tube of enzymes, the more rapid the reaction rate. Similar effects on enzymes, had been noted with high intensity magnetic fields. The strength of the magnetic fields utilized were approximately 13,000 gauss 26,000 times the intensity of the earth's magnetic field. The type of change in enzyme activity activity noted after exposure to healers was always in a direction of greater health of the cells, and thus of the organism. Whatever the enzyme used the healers always caused changes in activity which would result in a push to greater health and energy balance of the sick organism.Dr John Zimmerman at the University of Colorado has also demonstrated significant increases in the intensity of the magnetic fields emitted by healers hands⁵. The increase in magnetic field signals from healers hands were up to several times larger than background noise. However, again these fields were at intensity levels far weaker than those required to produce enzyme effects in the laboratory. The suggestion is that the subtle life-energies of healers seem to have primarily magnetic properties.

Dr Tiller theorizes that negative space/time is the domain of the etheric. A third substance called "deltron" has been hypothesized to act as an energy-bonding coupler between the etheric and physical worlds. Tiller feels that the postulation of this deltron intermediary was necessary because there are no resonant vibrational modes possible between etheric and physical energies in view of the fact there is no frequency overlap between positive and negative space/time. (This may not be actually the case as we know there can be interactions between higher and lower octave of energies, possible through resonant harmonic effects, as in the case of photographing the Phantom Leaf Effect). The important revelation is that we have a theoretical model of matter/energy relationships which begins to give us a mathematical foothold on the physical universe, the physical-etheric interface, and the world of etheric substance. What is most interesting about the entire positive-negative space/time diagram is that this model is predicted by Einstein's relativistic equation!

Dr Richard Gerber remarks in his book Vibrational medecine the following:

"The positive-negative space/time model appears very useful in demonstrating that modern physics may already have within its grasp the mathematical tools available to begin to understand these subtle energetic phenomena. This multidimensional energetic understanding of Einsteinian medecine may ultimately change the way we will view ourselves and the healing arts in the future."

Footnote

As a final note, I would like to say that as an energy practitioner, whilst researching this article and creating this web page, just thinking about the concepts of negative space/time and magnetic healing energies actually triggered energy sensations in my hands. The energy felt warm and liquid and flowed in and out of my hands. Normally, I would do energy raising exercises or Tai Chi movements to create this same level of energy awareness. Similarly, whilst practicing as an energy practitioner, when I collect energy with my left hand and channel with my right, in this process, I have a sensation of 'weight' on my hands. Thus, this article may seem very theoretical for some, but for me, healing energies are an everyday reality, which I want to understand. As an Honours graduate of Physics and Geophysics, I am particularly thrilled that I can take my scientific interest in a new direction. Indeed, as many other scientists are doing in research around the world.

Essay Notes

This essay was based on information provided from chapter4 of Vibrational Medecine, Human Multidimensional Anatomy, ISBN 1879181584. Where this article has provided references I have included them below. Furthermore Web sources are also detailed below:

1.C. Muses, "Working with the Hypernumber Idea," in Consciousness and Reality, ed. C. Muses and A. Young (New York: Avon Books, 1972), pp448-469.
2.L. Feldman, "Short Bibliography On Faster-Than-Light Particles (Tachyons)," American Journal of Physics, vol 42 (March 1974)
3. R. Miller, "Methods of Detecting and Measuring Healing Energies," in Future Science, ed. S. Krippner and J. White (New York: Doubleday & Co. 1977), pp. 431-444
4. Smith J., The Influence on Enyzme Growth by "Laying-on-of-Hands," The dimensions of Healing:A symposium (Los Altos, CA: Academy of Parapsychology and Medecine), 1972.
5. "New Technologies Detect Effects of Healing Hands," Brain/Mind Bulletin, vol. 10, no. 16 (September 30, 1985).

ENERGY & VIBRATION: A Basis for a New Paradigm by Julian Perry Link

Aura of LIVING water Link

Definitions Link

Susan Rennison September 2003,
revised in October 2007

Back to Science Articles Menu

If you want to know more about the new phenomena of Space Weather , Earth
changes and the impact on human consciousness, then you can obtain a copy of

Tuning the Diamonds: Electromagnetism & Spiritual Evolution

Home

Footnote

Essay Notes

Suggested further reading

Susan Rennison September 2003,
revised in October 2007

Science Talk: Towards a New Paradigm

Part II – The Subtle Planes of Matter

As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality.

Susan Joy Rennison quotes:

“Space Weather is now a fact of life.”

“We are all astronauts now!”

“We must spiritually evolve as part of the new terms & conditions for living on Earth.”

“Space Weather will force many changes in how we do business on this planet.”

NASA Press Release:

“Earth and space are about to come into contact in a way that's new to human history.”

“We're on the threshold of a new era in which space weather can be as influential in our daily lives as ordinary terrestrial weather.”

White House Executive Order:

Best of the Blog - Archives Joyfire Tag Cloud

Science Talk: Towards a New Paradigm

Part II – The Subtle Planes of Matter

As far as the laws of mathematics refer to reality, they are not certain, and as far as they are certain, they do not refer to reality.

Footnote

Essay Notes

Suggested further reading

Susan Rennison September 2003, revised in October 2007

Susan Joy Rennison quotes:

“Space Weather is now a fact of life.”

“We are all astronauts now!”

“We must spiritually evolve as part of the new terms & conditions for living on Earth.”

“Space Weather will force many changes in how we do business on this planet.”

NASA Press Release:

“Earth and space are about to come into contact in a way that's new to human history.”

“We're on the threshold of a new era in which space weather can be as influential in our daily lives as ordinary terrestrial weather.”

White House Executive Order:

Best of the Blog - Archives Joyfire Tag Cloud

Susan Rennison September 2003,
revised in October 2007